2020-02-05

Merge sort

알고리즘 강의를 들으며 시간 복잡도 까지 계산하여 더 정확하게 알게 되었다.
평소 space complexity 가 O(n) 인 in-place merge sort 를 나는 즐겨 사용하고 있었는데, 시간 복잡도가 높아지고 구현이 복잡해 져서 이득이 별로 없었다는걸 알게 됐다.
변형된 문제 풀이로 자신보다 작은 숫자가 앞에 몇개나 있는지 세는 문제 풀이도 들었다. leetcode 에서 봤었던 문제다. Count of Smaller Numbers After Self

시간 복잡도 계산

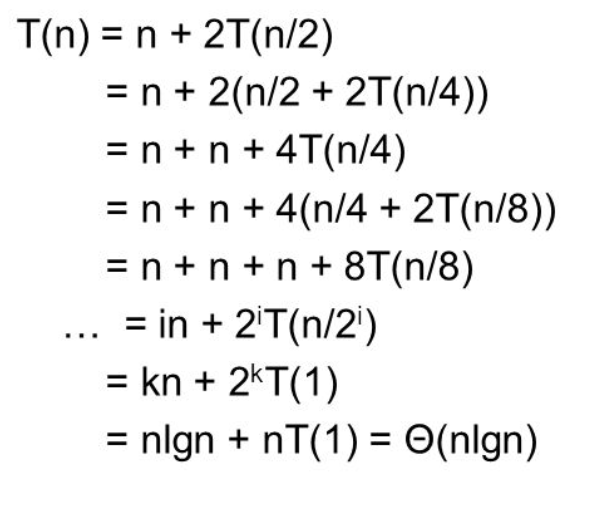
Merge sort

import random

def mergeSort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        left = arr[:mid]
        right = arr[mid:]
        mergeSort(left)
        mergeSort(right)
        
        # merge
        lenLeft = len(left)
        lenRight = len(right)
        leftIdx = 0
        rightIdx = 0
        for idx in range(0, lenLeft + lenRight):
            if rightIdx >= lenRight or (leftIdx < lenLeft and left[leftIdx] < right[rightIdx]):
                arr[idx] = left[leftIdx]
                leftIdx += 1
            else:
                arr[idx] = right[rightIdx]
                rightIdx += 1

for _ in range(10000):
    arr = [random.randint(1, 100) for _ in range(10000)]
    expect = sorted(arr)
    mergeSort(arr)
    assert arr == expect